| Маховик в виде тонкого обода |
| Физика маховичных двигателей | |||
| 05.04.2014 20:01 | |||
|
Для определения напряжений во вращающемся тонком ободе (кольце) применим известный из механики принцип Даламбера, позволяющий свести динамические процессы (т. е. процессы, связанные с движением тел) к равновесию. Для этого, правда, нам приходится добавлять к действующим на тело силам, силы инерции.
Рассечем мысленно маховик на две равные части и, убрав одну из них, заменим ее действие на оставшуюся часть силами F1 и F2, равными между собой.
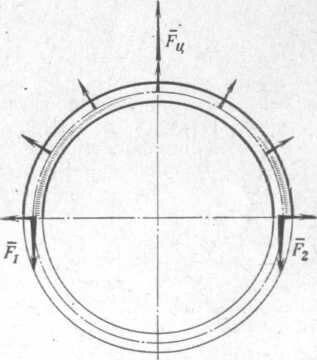
Полукольцо под действием центробежных сил
Что же вызывает возникновение этих сил? Если применять принцип Даламбера и рассматривать маховик как неподвижный, то нам надо, согласно сказанному выше, прикладывать к оставшейся части маховика силу инерции — центробежную силу. Она-то и вызывает силы F1 и F2, удерживающие полукольцо на месте.
Заменим действие полукольца действием точечной массы, равной массе полукольца и расположенной в центре тяжести (центре масс). Из геометрии известно, что центр тяжести полу-кольца расположен на расстоянии D/π от центра окружности, где D—диаметр обода. Величина центробежной силы Fц равна, как известно, произведению массы m на квадрат угловой скорости вращения ω и на расстояние этой массы от центра вращения, в данном случае D/π. Итак:
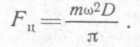
Сила же, разрывающая обод, F1=F2, будет в 2 раза меньше, так как Fц «удерживается» двумя равными силами F1 и F2. Учитывая это, а также то, что масса полукольца равна
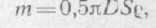
где g — плотность материала, а напряжение о равны отношению F к площади поперечного сечения S, имеем

Выразив окружную скорость v через угловую скорость и диаметр кольца D:υ =ωD/2, окончательно получим знакомую из предыдущего формулу
σ = gυ^2. (30)
Итак, для ободкового маховика напряжения не зависят от его размеров, а только от плотности материала и окружной скорости.
|